Aperçu des sections

  • Généralités

  • COURS

    • SIMILITUDES PLANES DIRECTES



      1 – Transformations du plan

      ·         Ce sont les applications bijectives du plan dans lui-même.

       

      ·         L’application réciproque d’une transformation est une transformation de même nature.

       

      ·         Le compose de deux transformations est une transformation.

       

      ·         L’image d’un objet géométrique par une transformation est un objet géométrique de même nature.

       

      2 – Exemples et caractéristiques de transformation

       

      M(x ; y) ; M’(x’ ; y’) ; Ω(a ; b) trois points du plan.  Δ une droite du plan.

       

      Si M’ est l’image de M par la transformation S alors le couple (M ; M’) est appelé couple de points homologues.

       

      a)     Symétrie centrale `SΩ`

       

      -          M’ =SΩ(M)\( \Leftrightarrow \)Ω est le milieu de[MM'];

       

      -          SΩ est caractérisé par son seul point invariant : son centre ;

       

      -      L'application réciproque SΩ est SΩ lui-même.

       

      b)     Symétrie axiale SΔ

       

      -          M’ =SΔ(M)\( \Leftrightarrow \) Δest la médiatrices de [MM']

       

      -          SD est caractérisé par son axe ;

       

      -          La réciproque de SΔ est  SΔ lui-même.

       

      -          RQ : le compose de deux symétries est l’identité.

       

      c)       Translation t

       

      -       ;

       

      -          Une translation est caractérisé par son vecteur  ;

       

      -          L’application réciproque de tu est t-u ;

       

      -          Le compose de deux translations est une translation tu+u’.

       

      d)     Homothétie h[Ω,k]

       

                 -      M'=h[Ω,k](M)\( \Leftrightarrow \) =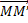

      -          Une homothétie est caractérisé par son centreΩet son rapport k

      (k≠0 et k≠1) ;


      -          L’application réciproque de h[Ω,k]  est de  h[Ω,1/k]].



      e)      Rotation r[Ω,θ]

          


      -  


       

      -          Une rotation est caractérisé par son centre Ω et son angleθ ;


      -          L’application réciproque der[Ω,θ]  est de r[Ω,-θ]   ;

       

      -          Le compose de deux rotations n’est pas forcément une rotation.



      3 – Similitudes planes directes S[Ω,k,θ]

       

      -          C’est le compose commutatif d’une homothétie et d’une rotation de même centre.

       

      -          Elle est caractérisée par son centre Ω, son rapport k et son angle θ ;

       

      -          Son application réciproque est caractérisée par son centre Ω, son rapport `1/k` et son angle -θ .


       

      4 – Equation analytique d’une similitude plane

      M(X ; Y) et M’(x’ ; y’). On a S : 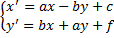 v    avec k =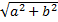 g


       

      cosθ =\( \frac{x}{k} \) et sinθ =\( \frac{y}{k} \)  et Ω est le seul point vérifiant Ω = SΩ.



       

      5 – Equation complexe d’une similitude plane directe

       

      M(z =x + yi) et M’(z’ = x’ + y’i), a et b deux nombres complexes connus.

       

      On a : z’ = az + b   avec k = 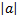a ,θ = arg(a) et `Ω(\( \omega \)=\( \frac{b}{1-a} \).



       

      6 - Nature de S suivant les valeurs de

       

      Si a = 1 alors S est la translation de vecteur d’affixe b ;

       

      Si a réel différent de 0 et de 1, alors S est l’homothétie de centre Ω et de rapport k = a ;

       

      Si a est un complexe tel que |a|=1  alors S est la rotation de centre Ω et d’angle ,θ;

       

      Si a est un complexe tel que |a| \( \neq \) 1   alors  S  est la similitude plane directe de centre Ω ,  de rapport  k  et  d’angle  ,       θ = arg (a).



       

      7 – Composition de deux similitudes planes directes

       

      S : z’ = az + b  et S’ : z’ = a’z + b’.

       

      SoS’ : z’’ = azS’ + b = a(a’z + b’) + b = aa’z + ab’ + b.

       

      S’oS : z’’ = a’zS + b’ = a’(az + b) + b’ = a’az + a’b + b’.

       

      8 – Equation d’une similitude définie par deux couples de points homologues

       

      (A (za); A’(za’)) et (B(zb) ; B’(zb’)) deux couples de points homologues.


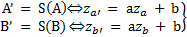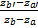      h`=>`a = f  et b = za’ – a za

       

       

       

       

       

       

      Auteur : RAKOTOARIVONY Toavinkaja Soloarivelo, enseignant au Lycée Andohalo , Classe de première et terminale


       

       

  • COURS VERSION PDF

  • EXERCICES