Themen dieses Kurses
- Allgemeines
- Chap II MOUVEMENT PERIODIQUE SINUSOIDAL
Chap II MOUVEMENT PERIODIQUE SINUSOIDAL
MOUVEMENT PERIODIQUE SINUSOIDAL
1- 1- Définitions :
- Un mouvement est périodique s’il se répète de façon identique à lui-même, à des intervalles de temps successifs égaux à T (période du mouvement)
- Un mouvement périodique est sinusoïdal si un point mobile M du mouvement effectue un mouvement de va-et-vient autour de sa position d’équilibre. L’élongation du mobile à l’instant t s’écrit : y = a sin (ωt + φ)
Exemple : mouvement d’un pendule simple


La longueur de la trajectoire est l = 2a
- Un mouvement périodique sinusoïdal est vibratoire s’il est très rapide. L’élongation des points vibrants satisfait à y = a sin (ωt + φ) ou y = a sin (
 t + φ) ou y
= a sin (2ΠNt + φ)
t + φ) ou y
= a sin (2ΠNt + φ)Exemple : vibration d’une lame élastique en acier
 OL :
lame vibrante
OL :
lame vibrante
- La période T du mouvement est la durée d’une oscillation complète.
- La fréquence N du mouvement est le nombre d’oscillations par seconde.
2- 2-Propagation d’un ébranlement :
Un ébranlement est une déformation brusque et locale ; il se propage avec une vitesse constante dans un milieu élastique (exemples : corde en caoutchouc, ressort, surface d’un liquide, …)
a) a) Ebranlement transversal :
· - Expérience :
Soit une corde en caoutchouc légèrement tendue. Faisons déplacer l’extrémité O de la corde vers O’.



La portion de la corde voisine de O se déforme, puis revient à l’équilibre pendant que la portion suivante se déforme à son tour et ainsi de suite. On dit qu’il y a propagation d’un ébranlement le long de la corde élastique.Au passage de l’ébranlement, chaque point de la corde se déplace perpendiculairement à la direction de propagation.
v - Définition :
L’ébranlement est dit transversal lorsque les points du milieu se déplacent perpendiculairement à la direction de propagation.
b) b) Ebranlement longitudinal :
v - Expérience :
Soit un long ressort très souple légèrement tendu.



A l’instant t = 0, le piston est en S, son élongation est alors supposée nulle. Toutes les spires du ressort sont équidistantes.
Faisons déplacer le piston vers la droite, le ressort se raccourcit ; ce sont seulement les spires voisines de S qui se rapprochent immédiatement en créant une zone comprimée.
Lorsque nous abandonnons le piston à lui-même, les spires près de S reprennent leur position initiale tandis que les spires voisines se compriment à leur tour et ainsi de suite. La compression se progresse le long du ressort.
Au passage de l’ébranlement, chaque spire du ressort fait un déplacement parallèle à la direction de propagation.
v - Définition :
L’ébranlement est dit longitudinal lorsque les points du milieu se déplacent parallèlement à la direction de propagation.
c) c) Ebranlement à la surface libre du liquide :
Un choc à la surface libre d’un liquide tranquille engendre une ride circulaire dont le rayon croît uniformément. Les rides circulaires se propagent dans toutes les directions avec la même vitesse.

d) d) Conclusion :
v La propagation d’un ébranlement ne correspond jamais à u transfert de matière.
v L’ébranlement se propage à vitesse constante. Cette vitesse constante de propagation s’appelle : célérité de propagation.
v On appelle célérité de propagation, la vitesse de propagation d’ébranlement d’un milieu élastique. La célérité dépend des constantes physiques et mécaniques du milieu propagateur.
3- 3- Expression de la célérité d’ébranlement :
a) a) Ebranlement transversal transmis par une corde tendue :
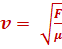
F : force de la tension de la corde (N)
μ : masse linéique de la corde (Kg.m-1)

v : célérité d’ébranlement
b) b) Ebranlement longitudinal transmis par un gaz :

p : pression du gaz
ρ: Masse volumique du gaz
 :
Rapport des chaleurs massiques à pression constante et à volume constant.
:
Rapport des chaleurs massiques à pression constante et à volume constant.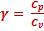
Cp : chaleur massique à pression constante
Cv : chaleur massique à volume constant
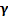 ne
dépend que de l’atomicité du gaz.
ne
dépend que de l’atomicité du gaz.§ Pour les gaz monoatomiques (He, Ne, Ar,…)
 = 1,67
= 1,67§ Pour les gaz diatomiques (H2, N2, O2,…)
 = 1,33
= 1,33Remarque :
Au passage d’ébranlement, chaque point du milieu reproduit le mouvement de la source.

Un point M situé à la distance x de la source O, reproduit le mouvement de O avec un retard de
 , θ est
appelé décalage horaire.
, θ est
appelé décalage horaire.4- 4- Longueur d’onde λ :
On appelle longueur d’onde, la distance parcourue par l’onde pendant une période T.
 ou
ou 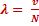
λ est exprimé en m.
v en m.s-1
N en Hz et T en s.
5- 5- Propagation d’un mouvement vibratoire sinusoïdal le long d’une corde :
a) a) Onde progressive dans un milieu unidimensionnel :
· - Observation du mouvement de la corde :
·

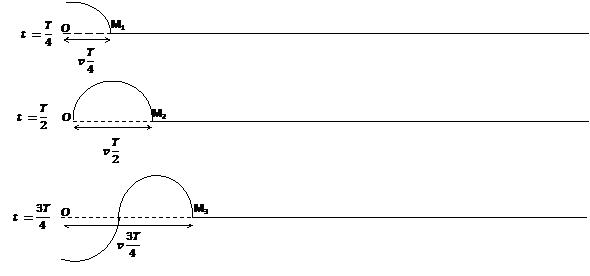
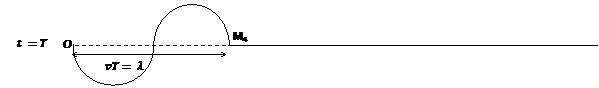
On obtient une sinusoïde qui reproduit les variations de l’élongation du point M en fonction du temps : c’est la sinusoïde des temps.
On obtient aussi une sinusoïde qui donne la position de tous les points de la corde à un instant donné : c’est la sinusoïde des espaces.
On appelle onde progressive l’ensemble des perturbations obtenues sur le milieu par la propagation du mouvement vibratoire.
· - Interprétation :
- Périodicité dans le temps :
Chaque point de la corde s’anime d’un mouvement sinusoïdal de même amplitude a et de même période T. Le graphe y = f(t) est la sinusoïde des temps.
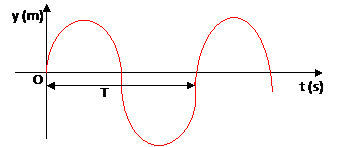
y = a sin (ωt) = y = a sin (
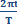 t)
t)- Périodicité dans l’espace : longueur d’onde
Chaque point de la corde s’anime d’un mouvement sinusoïdal de même amplitude a et de même période spatiale λ(longueur d’onde). Le graphe y = f(x) est la sinusoïde des espaces.
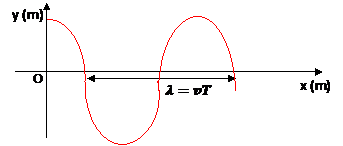
Le point M situé à la distance x de la source O reproduit le mouvement de o avec un retard de
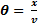
Soit yM(x) = y(t –
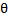 )
)yM(x) = a sin [ω(t –
 )]
)]yM(x) = a sin[
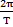 (t
-
(t
-  )]
)]yM(x) = a sin[
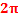 (
( -
- 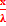 )]
)]· - Deux vibrations le long d’une corde :
Soit deux points M1 et M2 d’une corde de longueur l et d’équations horaires respectives :
y1 = a sin(
 -
-  ) avec
) avec  = -
= - 
y2 = a sin(
 -
- 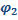 ) avec
) avec 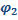 = -
= - 
La différence de phase entre y1 et y2 s’écrit 𝚫φ =
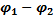
- - Points vibrants en phase :
M1 et M2 vibrent en phase si
 =
2kπ, kϵ
=
2kπ, kϵ 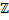
-
 +
+ 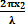 =
2kπ
=
2kπx2 – x1 = kλ, kϵ
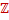
Deux points distants d’un nombre entier de longueur d’onde vibrent en phase
- - Points vibrants en opposition de phase :
M1 et M2 vibrent en opposition de phase si
 =π
+ 2kπ, kϵ
=π
+ 2kπ, kϵ 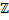
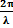 (x2
– x1) = π + 2kπ
(x2
– x1) = π + 2kπx2 – x1 = (2k + 1)
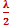
Deux points distants d’un nombre impair de demi-longueur d’onde vibrent en opposition de phase.
- - Points vibrants en quadrature de phase :
M1 et M2 vibrent en quadrature de phase si
 =±
=± +
2kπ, kϵ
+
2kπ, kϵ 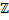
v y y1 est en quadrature avance sur y2 si
 =
=  +
2kπ
+
2kπ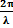 (x2
– x1) =
(x2
– x1) =  +
2kπ
+
2kπx2 – x1 = (2k +
 )
)
v y1 est en quadrature retard sur y2 si
 =
-
=
-  +
2kΠ
+
2kΠ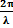 (x2
– x1) = -
(x2
– x1) = -  +
2kπ
+
2kπx2 – x1 = (2k -
 )
)

