Aperçu des sections
- Généralités
- CINEMATIQUE
CINEMATIQUE
CINEMATIQUE
Mécanique= Cinématique + Dynamique
1. Introduction
La cinématique est l’étude des mouvements sans se préoccuper des causes responsables de ces mouvements.
Grandeurs étudiées :
- - Position
- - Trajectoire
- - Vitesse
- - Accélération
Cette étude du mouvement s’effectue selon l’une des deux formes :
- vectorielle : en utilisant les vecteurs : position
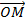 l’accélération
l’accélération- - algébrique : en définissant l’équation du mouvement suivant une trajectoire donnée.
2.
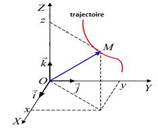
 Position du mobile
Position du mobileLa position d’un point matériel M au temps t est repérée dans un repère
R (0,
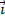 ,
, 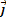 ,
,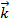 ) par un vecteur
) par un vecteur 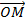
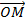 = x
= x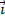 +y
+y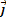 + z
+ z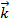
3- Equations horaires
Un point matériel est en mouvement si ses coordonnées varient en fonction du temps.
Ces coordonnées peuvent être notées par : x(t), y(t), z(t).On appelle ces fonctions, les équations horaires du mouvement. On peut les exprimer sous la forme : x=f(t) ; y=g(t) et z=h(t).
4. Trajectoire
On appelle trajectoire du point (M) d’un solide (S) l’ensemble des positions occupées successivement par ce point, au cours du temps, au cours de son déplacement par rapport à un référentiel donné.
L’équation y=f(x) s’appelle équation cartésienne de la trajectoire.
On obtient l’équation de la trajectoire par élimination du temps entre les deux équations horaires.
5. Vitesse
On considère que la vitesse est la distance parcourue par unité de temps.
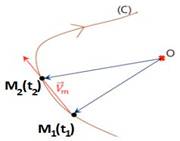
a. Vecteur vitesse moyenne

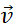 =
= 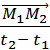
b. Vecteur vitesse instantanée
Le vecteur vitesse instantanée, c'est à dire au temps t, est la dérivée du vecteurposition par rapport au temps :
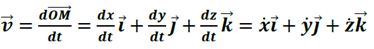
Caractéristiques de :
- Point d’application : point M où l’on veut définir la vitesse ;
- Direction : tangente à la trajectoire ;
- Sens : celui du mouvement ;
-
 Norme :
Norme : 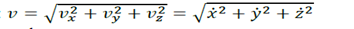
Unité : m.s-1
c. Cas de l’abscisse curviligne
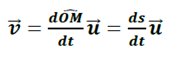


6. Accélération
Nous considérons que l’accélération est la variation de la vitesse par unité de temps.
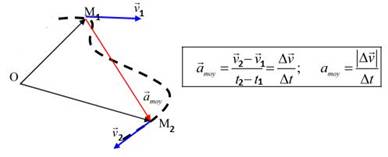
a. Vecteur accélération moyenne

b. Vecteur accélération instantanée
Le vecteur accélération instantanée d’un mouvement est défini comme étant la dérivée du vecteur vitesse instantanée par rapport au temps.
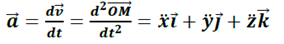
Module :
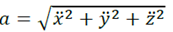
̈Unité : m.s-2

c. Vecteur accélération et base de FRENET
Soit
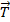 le vecteur unitaire tangent en M à
la trajectoire et orienté dans le sens du mouvement.
le vecteur unitaire tangent en M à
la trajectoire et orienté dans le sens du mouvement.Soit
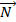 le vecteur unitaire orthogonal à
le vecteur unitaire orthogonal à 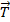 et orienté vers l’intérieur de la trajectoire.
et orienté vers l’intérieur de la trajectoire.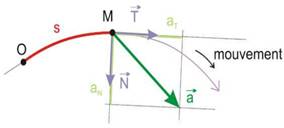

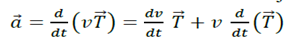
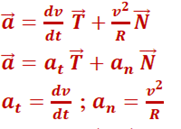
La base (
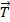 ,
, 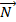 ) constitue la base de Frenet R (M,
) constitue la base de Frenet R (M, 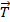 ,
, 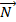 ) est le repère de Frenet.
) est le repère de Frenet.

7. Mouvement accéléré, retardé ou uniforme
Un mouvement est dit accéléré si le module de
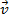 augmente ;
augmente ;
Un mouvement est dit décéléré si le module de
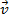 diminue;
diminue; 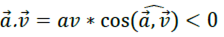
Un mouvement est dit uniforme si le module de
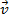 reste constante ;
reste constante ;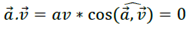
8. Étude de quelques mouvements
a. MRU, MRUV, MCU et MCUV
Mouvement rectiligne
Mouvement circulaire
Mouvement rectiligne uniforme (MRU)
Trajectoire : droite
x = vt + x0
v = constante
a = 0
Mouvement circulaire uniforme (MCU)
Trajectoire : cercle
θ =
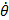 t + θO
t + θO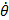 = constante
= constante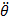 = 0
= 0Mouvement rectiligne uniformément varié (MRUV)
x =
 at2+v0t + x0
at2+v0t + x0v = at + v0
a = constante
RIT *: v2 – v02 = 2a(x – x0)
Mouvement circulaire uniformément varié (MCUV)
θ =
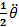 t2 +
t2 + 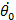 t + θO
t + θO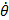 =
= 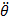 t +
t + 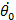
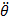 = constante
= constanteRIT *:
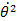 -
-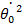 = 2
= 2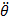 (θ –
θ0)
(θ –
θ0)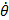 : vitesse angulaire
: vitesse angulaire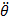 : accélération angulaire
: accélération angulairex = Rθ , v = R
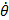 , a = R
, a = R 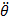
*RIT : Relation Indépendante du Temps
b- Mouvement rectiligne sinusoïdal
Un mouvement rectiligne est dit sinusoïdal lorsque son équation horaire est de la forme x(t)= xmsin(ωt+𝞿 ).
x : élongation ou abscisse à l’instant t (en m);
xm: amplitude maximale du mouvement (toujours positive);
ω: pulsation ou vitesse angulaire du mouvement (en rad/s);
(ωt+𝞿) : phase à l’instant de date t (en rad);
𝞿 : phase à l’origine (en rad).
Vitesse :
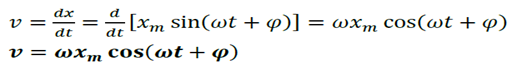
Accélération :
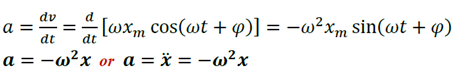
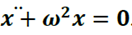
C’est une équation différentielle caractéristique du mouvement rectiligne sinusoïdal
c- Mouvement circulaire sinusoïdal :

Période T
C’est le temps nécessaire pour faire un tour complet.
T =
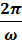 oùT en s etωen rad.s-1
oùT en s etωen rad.s-1Fréquence du mouvement
C’est le nombre de tour par seconde.
F =
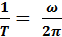 où F en Hz (Hertz) et T en s
où F en Hz (Hertz) et T en s
Relation entre θ et le nombre de tour n :
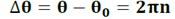
Relation entre ω et le nombre de tours par seconde N :
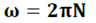

Mr RANDRIANANTENAINA Chabanas Deloy
e mail: deloychabanas@gmail.com
