Topic outline

  • General

  • COURS

    • Calculs de limites

      Pour calculer une limite, on change tout simplement la valeur de la variable par la valeur donnée.
      Attention, l’un des résultats suivant est une forme indéterminée :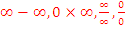 1.
      Les méthodes les plus courant de lever l’indétermination est de :
      • factoriser  ou appliquer la règle de l’Hospital pour lever le 2;
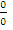      • utiliser les fonctions équivalentes pour beaucoup de cas.

      On dit que f est équivalente a g au voisinage de x0 lorsque la limite de leur quotient vaut 1 quand x tend vers x0.
      Dans les calculs de limites, on peut remplacer l’expression de f par celle de g. Notation .
      Règle de l’Hospital :
      Soient N et D deux fonction dérivable et f la fonction définie par  où N’ est la dérivée de N et D’ la dérivée de D.
      Fonctions équivalentes

        • Au voisinage de l’infini, un polynôme est équivalent à son terme du plus haut degré ;
        • Au voisinage de zéro, un polynôme est équivalent ç son terme du plus bas degré ;
        • Au voisinage de zéro, on a :

        Continuité


        Pour les fonctions définies par morceaux, il est nécessaire de calculer les limites à gauche et à droite en x0. Pour que la fonction soit continue en x0, ces deux limites doivent être égales à l’image dex0 par f.


        La fonction f est continue sur un intervalle I inclus dans son ensemble de définition si et seulement si f est continue en tout a de I.

        • Théorèmes généraux

        Soient f et g deux fonctions continues sur un même intervalle I. Alors :
                        * f + g est continue sur I ;
                        * kf où k est un réel non nul est continue su I ;
                        * fg est continue sur I ;
                        * Si de plus g est non nulle sli>ur I, alors sont continues sur I ;
                        * Si f est continue sur I et g continue sur f(I), alors g o f est continue dur I.

        • Exemples
        • Toute fonction polynôme est continue sur ¡ ;
        • Toute fonction rationnelle ou irrationnelle est continue sur tout intervalle contenu dans son ensemble de définition.
        • Théorème des valeurs intermédiaires

        Soit f une fonction continue sur un intervalle I contenu dans son ensemble de définition et soient a et b deux réels de I tels que a < b. Pour tout réel k entre f(a) et f(b) alors il existe au moins un réel  tel que f(c) = k.
        Autrement dit, pour tout k entre f(a) et f(b), l’équation f(x) = k admet au moins une solution dans 

        Branches infinies

        Condition

        La courbe représentative de la fonction f admet une branche infinie lorsque se trouve dans l’ensemble de définition ou après calcul de limite.

        Classification
      • La droite (horizontale) D :  
      • La droite (verticale) D’ :

        • C1 : si de direction Ox) ;
        C2 :si de direction Oy) ;
        C3. 
                    C31. Si q est un réel ;  alors D’’ d’équation y = px + q est asymptote oblique  à la courbe ;
                    C32. Si q =\( \infty \)alors la courbe admet une branche parabolique oblique de direction y = px ou bien de coefficient directeur p.

        Autre possibilité

         En cas de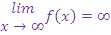h, si on peut écrire f(x) sous la forme f(x) = g(x) + \( \epsilon \)(x) avec  alors la courbe d’équation y = g(x) est asymptote à la courbe de f au voisinage de l’infini.

        Remarque

        Une n’est pas forcément une droite. Elle peut être une courbe. D’habitude c’est l’une des courbes des fonctions de référence qu’on a vues en classe de seconde.

        Position de la courbe par rapport à son asymptote

        Soit C : y = f(x) et D : y = px + q. Les positions relatives de C par rapport à D s’obtiennent =en étudiant les signes de d(x) = f(x) – (pq + q).

        1. Si d(x) = 0, les deux courbe se coupent ;
        2. Si d(x) > 0 sur un intervalle I alors C est au-dessus de D ;
        3. Si d(x) < 0 sur I alors C est au-dessous de D.








  • COURS VERSION PDF

  • EXERCICES

    • representation graphique