Aperçu des sections
- Généralités
- ChapI FONCTIONS SINUSOIDALES
ChapI FONCTIONS SINUSOIDALES
FONCTIONS SINUSOIDALES
1- 1- Définition :
Une fonction sinusoïdale de temps est une fonction de la forme : y = a sin (ωt + ϕ) où a, ω et ϕ sont des constantes.
y : élongation du mobile à l’instant t(m)
a : amplitude ou élongation maximale (m)
-a
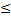y
aω : pulsation du mouvement (rad.s-1)
φ : phase à l’origine des temps (t=0) (rad)
ωt + φ : phase à l’instant t(rad)
2- 2-Périodicité :
La fonction sinusoïdale y(t) est périodique, de période T =
T en secondes(s)
ω en rad.s-1
On appelle période T, l’intervalle de temps constant qui sépare deux passages successifs du mobile animé d’un mouvement d’oscillations, en un même point et dirigeant dans le même sens.
Exemple : y(t) = 3 sin (
)
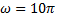rad.s-1T =
= 
=
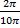0,2s3- 3- Représentation de Fresnel :
Définition :
A toute fonction y = a sin (ωt + φ), on associe un vecteur tournant
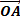de
longueur a, faisant un angle φ avec l’origine des phases à l’instant t=0
et qui tourne dans le sens trigonométrique autour de son origine O, avec une
vitesse angulaire constante ω.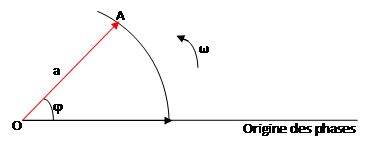
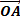pris
à l’instant t=0 est appelé vecteur tournant.φ : phase initiale du mouvement
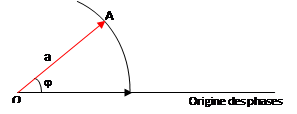
Exemple : y(t) = 3 sin (10πt +
)a = 3cm
φ =
rad
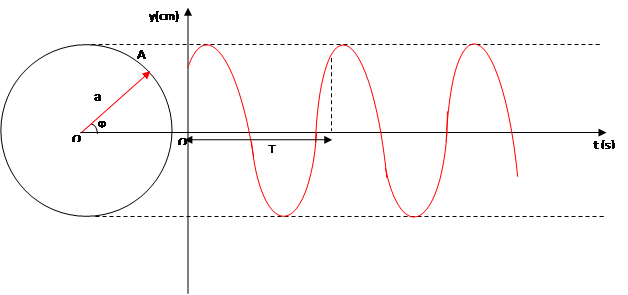
4- 4- Représentation graphique :
La fonction sinusoïdale y(t) est représentée par une sinusoïde. A tout mouvement circulaire uniforme, on peut faire correspondre un mouvement rectiligne sinusoïdal et inversement.
Exemple : y(t) = 3 sin (10πt +
)T= 0,2s
5- 5- Déphasage (ou différence de phase) de deux fonctions sinusoïdales :
Soit deux fonctions sinusoïdales de même période :
y1 = a1 sin (ωt + φ1) de vecteur de Fresnel
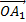
y2 = a2 sin (ωt +φ2) de vecteur de Fresnel
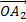
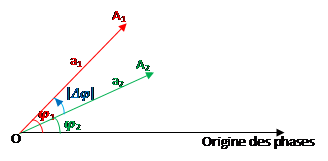
La différence de phase
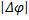est
donnée par :
=
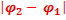
Cas particuliers :
- Si 𝚫φ = 2kΠ, kϵℤ, y1 et y2 sont en phase ou en concordance de phase. Les deux fonctions y1 et y2 sont représentées par deux vecteurs de même direction et de même sens.
- Si 𝚫φ = Π + 2kΠ, kϵℤ, alors y1 et y2 sont en opposition de phase. Les deux fonctions y1 et y2 sont représentées par deux vecteurs de même direction mais de sens contraire.
- Si 𝚫φ = ±
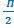+ 2kΠ, kϵℤ, alors y1
et y2 sont en quadrature de phase.
Les deux fonctions y1 et y2 sont représentées par deux
vecteurs orthogonaux.φ1 – φ2 =
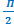+ 2kΠ, y1 est en quadrature avance sur y2.φ1 – φ2 = -
+ 2kΠ, y1 est en quadrature retard sur y2.6- 6- Vitesse algébrique :
C’est la dérivée de la fonction sinusoïdale par rapport au temps t.
y = a sin (ωt + ϕ)
v =
= 
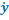= aωcos(ωt
+ ϕ)7- 7- Somme de deux fonctions sinusoïdales de même période :
Soit deux fonctions sinusoïdales de même période.
y1 = a1 sin (ωt + φ1) de vecteur de Fresnel
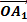
y2 = a2 sin (ωt +φ2) de vecteur de Fresnel
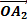
y1 et y2 sont les vibrations composantes.
La somme de ces deux fonctions sinusoïdales est une fonction sinusoïdale y = y1 + y2
y= a sin (ωt + φ) de vecteur de Fresnel
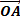
y est la vibration résultante.
= 
+ 
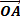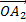
Amplitude a :
= + 
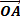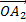
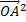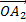=(+ )2
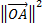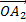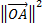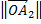=(+ )2=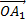
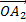
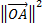2
+
2
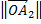+ 2
.= 2
+ 2+2
.cos(, 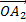)a2=
+ 
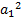+ 2
a1.a2.cos(φ2
- φ1)a =
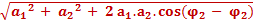
Phase φ :
tan φ =
=
=
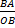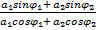
tan 𝞿 =
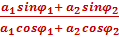
Cas particuliers :
a) Vibration en concordance de phase :
φ2 - φ1 = 2kΠ, kϵℤ ⟹φ2= φ+ 2kΠ
y = y1 + y2
= a sin (ωt + φ)
a = a1 + a2
= 1 = 2La vibration résultante est en phase avec les vibrations composantes.
b) Vibration en opposition de phase :
φ2 - φ1 = Π + 2kΠ, kϵℤ ⟹φ2= φ1+Π + 2kΠ
y = y1 + y2
= a sin (ωt + φ)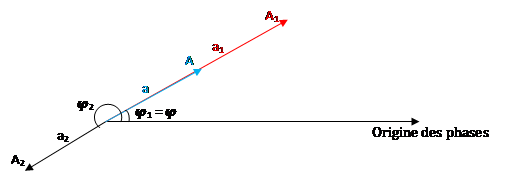
a =
φ = φ 1 ou φ = φ 2
La vibration résultante est en phase avec la vibration composante de plus grande amplitude.
c) Vibration en quadrature de phase :
φ2 - φ1 =
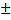
+ 2kΠ, kϵℤ y = y1 + y2
= a sin (ωt + φ)
a =
tan φ =
Résumé :
Cas
Solutions
Concordance de phase
Opposition de phase
Quadrature de phase
Cas général
A Amplitude
a = a1 + a2
a =
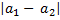
a =
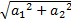
a =
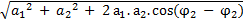
P Phase φ
=1
= 2φ = φ1 ou
φ = φ2
tan φ =
tan φ =
