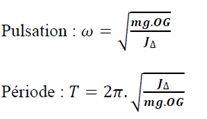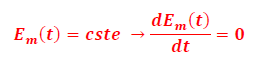Themen dieses Kurses
- Allgemeines
- DYNAMIQUE DE ROTATION
DYNAMIQUE DE ROTATION
MOUVEMENT DE ROTATION AUTOUR D’UN AXE
1- Théorème de l’accélération angulaire
1.1. TCI appliqué à un point matériel M en mouvement circulaire
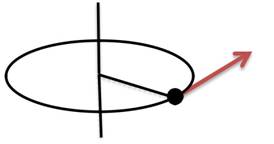
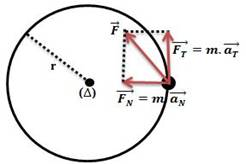
Soit un point matériel M de masse m en mouvement circulaire. (Δ) un axe perpendiculaire au plan de la trajectoire et passant par le centre O. Soit
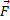 la résultante des forces extérieures
appliquées à M.
la résultante des forces extérieures
appliquées à M.D’après le TCI :
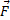 =m.
=m.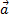
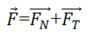

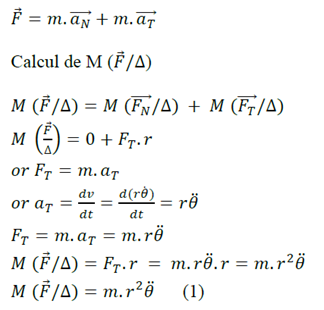
La quantité
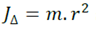 s’appelle moment d’inertie du
point matériel M par rapport à l’axe (Δ).
s’appelle moment d’inertie du
point matériel M par rapport à l’axe (Δ).
1.2.TCI appliqué à un solide en mouvement de rotation : TAA
Soit un solide (S) mobile autour d’un axe fixe (Δ) avec une accélération angulaire
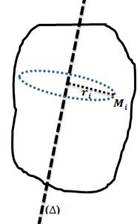
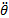 .Considérons un point Mi
de masse mi du solide. Le point Mi décrit une trajectoire
circulaire de rayon ri.
.Considérons un point Mi
de masse mi du solide. Le point Mi décrit une trajectoire
circulaire de rayon ri.
Soit
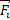 la résultante des forces extérieures
appliquées au point Mi.
la résultante des forces extérieures
appliquées au point Mi.D’après la relation (1) :
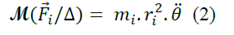
La somme des moments de forces extérieures qui s’exercent sur le solide (S) est égale à la somme des moments des forces qui s’exercent sur chacun des points Mi.
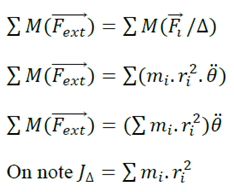
JΔest appelé moment d’inertie du solide (S) par rapport à l’axe (Δ).
On a :
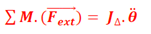 T.A.A
T.A.AD’où le TAA :
« La somme des moments des forces extérieures appliquées à un solide en mouvement de rotation est égale au produit de l’accélération angulaire par le moment d’inertie du solide par rapport à l’axe de rotation. »
2- 2- Quelques solides homogènes par rapport à un axe passant par son centre d’inertie G
2.1.Circonférence pesante/cylindre creux (jante, anneau, cerceau)
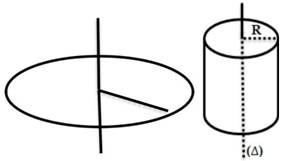
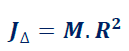
2.2. Disque de rayon R et de masse M
M : masse et R : rayon
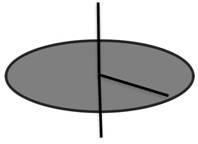
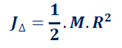
2.3.Cylindre plein de rayon R et de masse M

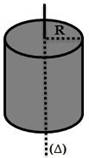
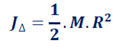
2.4. Sphère de rayon R et de masse M
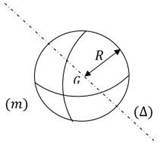
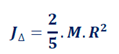
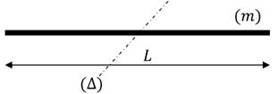
2.5. Tige de longueur L et de masse m

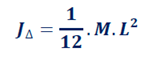
3. Théorème d’Huygens
Si l’axe de rotation ne passe pas par le centre d’inertie G, on utilise le Théorème d’Huygens pour trouver le moment d’inertie par rapport à cet axe.
Soit un solide de masse total M mobile autour d’un axe (Δ’) qui ne passe pas par son centre d’inertie G.

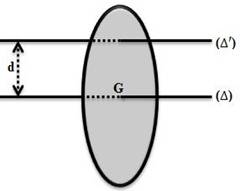
Le moment d’inertie de ce solide par rapport à l’axe (Δ’) est donné par le théorème d’Huygens :
JΔ: moment d’inertie par rapport à (Δ)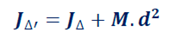
d : distance entre (Δ) et (Δ’)
Exemple :
Calculer le moment d’inertie d’un disque homogène de rayon R=10cm et de masse M=500g par rapport à un axe (Δ’) situé à une distance d =
 de son centre d’inertie G.
de son centre d’inertie G.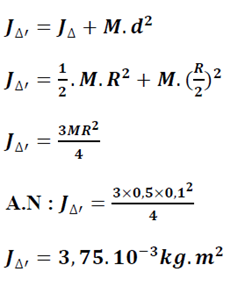
 4. Machine d’Atwood
4. Machine d’AtwoodDeux masses m1 et m2 sont reliées par un fil inextensible de masse négligeable qui passe par la gorge d’une poulie de masse m et de rayon r.
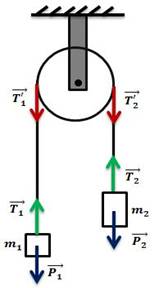

On suppose que la masse M de la poulie est uniformément repartie sur sa circonférence et que les forces de frottement sont négligeables. Déterminer l’accélération du mouvement de deux masses m1 et m2.
Etudions séparément le système :
Système 1 : {masse m1}
Système 2 : {masse m2}
Système 3 : {masse poulie}
Les systèmes (1) et (2) sont animés de mouvement de translation.
Système 1 :
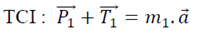
Projection sur un axe vertical ascendant :
-P1+T1=m1a (1)
Système 2 :
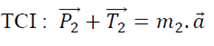
Projection sur un axe vertical ascendant :

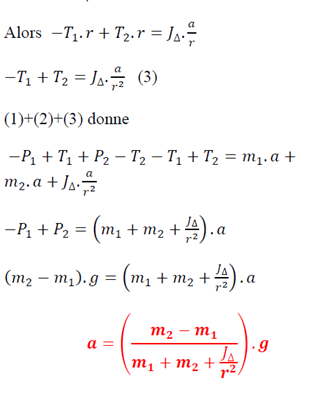

5. Pendule élastique de torsion
Un pendule de torsion est constitué par un solide S fixé à un fil de torsion. Ecarter de sa position d’équilibre et abandonner sans vitesse initiale, lesolide (S) effectue des oscillations autour de l’axe (Δ) qui est constitué par le fil de torsion lui-même. Ces mouvements d’oscillations sont assurés par le couple de torsion que le fil exerce sur (S).
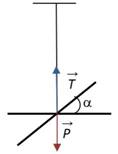
5.1. Etude dynamique
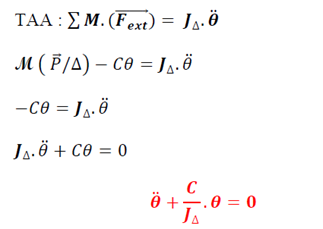
C’est l’équation différentielle du mouvement.
Nature du mouvement : mouvement de rotation sinusoïdal par rapport au fil.
L’équation horaire du mouvement:
 θ = θmsin(ωt
+φ )
θ = θmsin(ωt
+φ )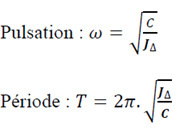
5.2. Energie mécanique
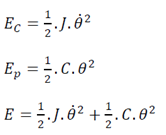
Le système {solide +fil de torsion +Terre} est un système isolé, alors l’énergie mécanique est conservée.
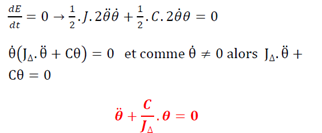
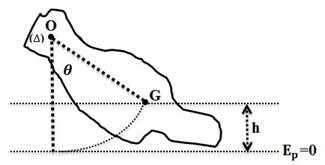
6. Pendule pesant
6.1. Définition
Un solide oscillant autour d’un axe horizontal fixe sous la seule action de son poids constitue un pendule pesant.
Exemple : le balancier d’une horloge, …

6.2. Etude dynamique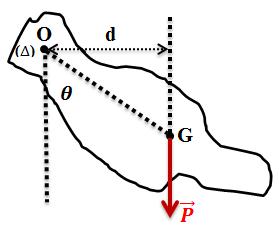
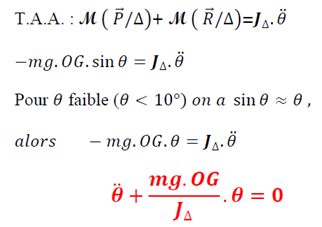
Nature du mouvement : mouvement de rotation sinusoïdale
Equation horaire :θ(t) = θmsin(ωt +φ)
6.3. Energie mécanique

7. Pendule simple synchrone (PSS) d’un pendule pesant
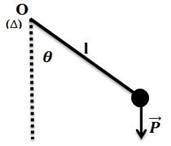
7.1. Pendule simple
Un pendule simple est un pendule constitué par une masse ponctuelle m suspendue à une tige ouun fil de masse négligeable de longueur l dont l’autre extrémité est accrochée à un point fixe O.
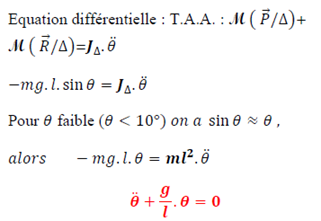
Nature du mouvement : mouvement de rotation sinusoïdale
Equation horaire :θ(t) = θmsin(ωt +φ)
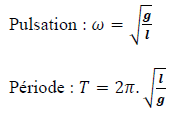
7.2.Pendule simple synchrone d’un pendule pesant
C’est un pendule simple qui a la même période que le pendule pesant.

l: longueur du PSS du pendule pesant
ENERGIE MECANIQUE
1. Energie cinétique EC
1.1. Energie cinétique de translation
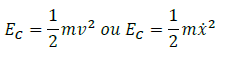
1.2. Energie cinétique de rotation
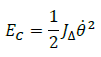
2. Energie potentielle EP
2.1. EP de pesanteur
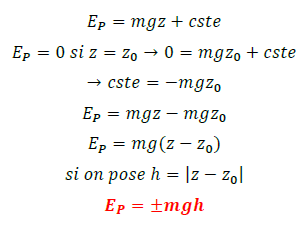
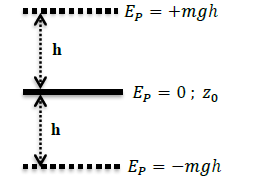
2.2. EP élastique (ressort)
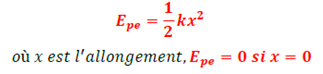
Remarque : Travail de la tension du ressort entre la position (1) et la position (2)
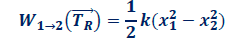
2.3. EP de torsion
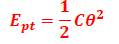
θ : angle à partir de sa position d’équilibre
C : constante de torsion
Remarque : Travail du couple de torsion entre la position (1) et la position (2)
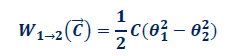
2.4. EP électrique d’une charge q
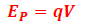
V : potentiel du point considéré.
3. Energie mécanique totale
Em = Ec + Ep
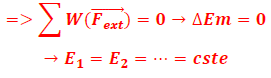
3.1. Système isolé
Un système est mécaniquement isolé lorsqu’il n’est soumis à aucune force extérieure.
L’énergie mécanique est conservée.
Un système est dit isolé lorsque son énergie mécanique est conservée.
Système isolé ⇾Em = constante
Un système isolé qui conserve l’énergie mécanique est tout système où il n’y a pas defrottement et pas de force motrice.
Les seules forces qui travaillent sont le poids
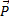 , la
, latension du ressort
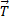 et le couple de torsion
et le couple de torsion 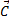 .
.Si l’Em est conservée, alors
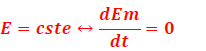
N.B : Dans la pratique, on prend comme système l’ensemble {corps + Terre + ressort ou fil de torsion} puis on applique la conservation de l’énergie mécanique.
3.2.Utilisation de la conservation de l’énergie mécanique
a) Première forme d’utilisation
Em = Ec + Ep = constante
Alors si EC augmente, EP diminue et vice versa.
b) 2ème forme d’utilisation
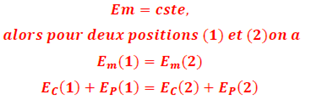
c) 3ème forme d’utilisation
PROBLEME DE CHOC
1. Choc mou
Un choc est mou lorsqu’ après le choc, les deux solides se collent et ont la même vitesse.
Soient deux solides de masse respective mA et mB qui entrent en choc.
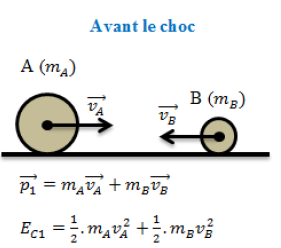

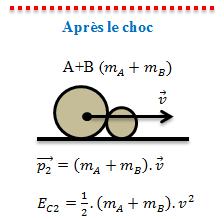
Choc mou, on a:
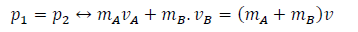
2. Choc parfaitement élastique
Un choc est parfaitement élastique lorsque après le choc, les deux solides se séparent et ont chacune sa vitesse.
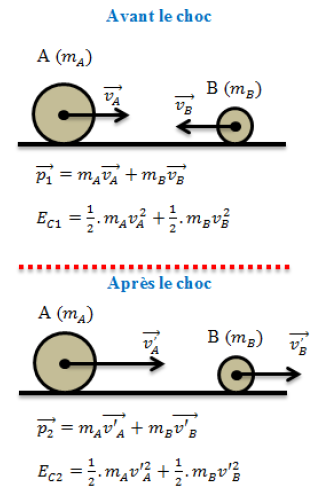
Choc parfaitement élastique :
p1 = p2
Ec1 = Ec2

Mr RANDRIANANTENAINA Chabanas Deloy
e mail: deloychabanas@gmail.com