Topic outline
- General
- Chap III INTERFERENCES MECANIQUES
Chap III INTERFERENCES MECANIQUES
INTERFERENCES MECANIQUES
1- 1- Principe de la superposition des petits mouvements dans un milieu élastique :
Supposons qu’une cause impose à un point M du milieu un petit déplacement
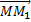 à
partir de la position d’équilibre et qu’une autre cause agissant seule provoque
au même point M un petit déplacement
à
partir de la position d’équilibre et qu’une autre cause agissant seule provoque
au même point M un petit déplacement 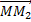 .
.Si les deux causes agissent simultanément, on constate que le déplacement effectué par le point M est
 ,
diagonale du parallélogramme construit avec
,
diagonale du parallélogramme construit avec 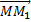 et
et 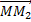 comme
côtés. Ceci se traduit par la relation vectorielle :
comme
côtés. Ceci se traduit par la relation vectorielle : =
= 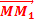 +
+ 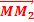
2- Interférences à la surface libre d’un liquide :a) a) Dispositif expérimental :
Une fourche est fixée à une lame vibrante. Les deux pointes de la fourche trempent légèrement dans l’eau d’une large cuve.
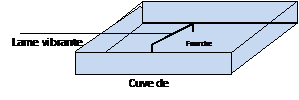
Lorsque la lame vibrante effectue un mouvement de vibration, les points O1 et O2 de la surface libre de l’eau, en contact avec les points de la fourche, constituent deux sources de vibrations sinusoïdales de même période et de même direction, de même amplitude et vibrant en phase.
b) b) Faits observés :
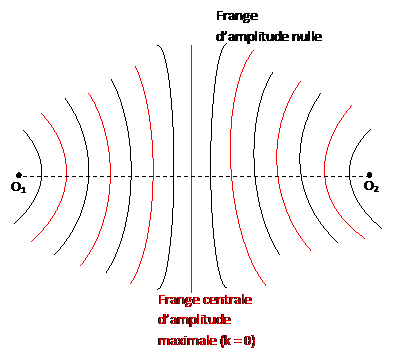
Sur la surface libre de l’eau, on observe des rides fixes, bien nettes dans la région voisine de la médiatrice du segment O1O2. Ces rides ont la forme d’arcs hyperboles dont les foyers sont O1 et O2. On les appelle des lignes ou des franges d’interférence.
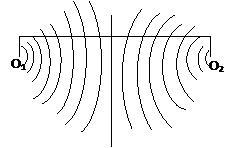
c) Interprétation :Les franges d’interférences résultent de la superposition de deux mouvements vibratoires de même période et de même direction, provenant de deux sources en phases O1 et O2 et se propageant sur la surface libre.
Les deux sources O1 et O2 ont même mouvement d’élongations :
yO1= yO2=
 t)
t)On dit qu’elles sont synchrones.
Considérons un point M de la surface libre du liquide situé à une distance d1 de O1 et à une distance d2 de O2.

Si la source O1 existait seule, l’élongation y1 du point M est
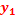 =
=  t -
t - 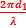 ) soit
) soit 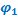 = -
= - 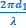
Si la source O2 existait seule, l’élongation y2 du point M est
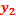 =
=  t -
t - 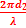 ) soit
) soit 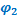 = -
= - 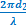
Lorsque les deux sources agissent simultanément, l’élongation y du point M est :
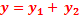 = A sin (
= A sin (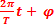 )
)A et φ sont déterminés à partir de la construction de Fresnel.


 =
=  +
+ 

v ( (OM1M2) est un triangle isocèle,
φ= φ2-
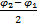 =
=  =
=  (-
(-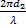 -
- 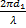 )
=-
)
=- 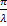 (
( )
)φ =
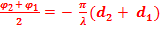
v (OIM1) est un triangle rectangle en I
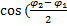 )=
)=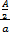 =
= 
A =
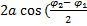 )
=
)
= 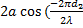 +
+  )
) A =
 ) =
) = 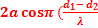 )
)Soit
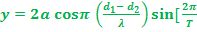 t
t ]
]3- 3- Etats vibratoires des points de la surface du liquide :
a) a) Points d’amplitude maximale :
A est maximale si
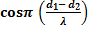 =
±1
=
±1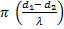 =
= 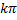 ,
, 
 =
= 
y1 et y2 sont en phase. Les points pour lesquels les mouvements composants sont en phase ont une amplitude maximale.
- Nombre de franges :

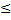 d1
– d2
d1
– d2 

d1 = +
+

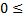 d1
d1  ⟹
⟹ 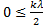 +
+  ⟹
⟹ 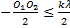
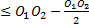 ⟹
⟹ 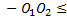

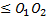
 k
k 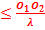
b) b) Point d’amplitude nulle :
A = 0 si
 =
0
=
0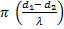 =
=  +
+ 
 = k +
= k + 
 =
= 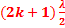
y1 et y2 sont en opposition de phase. Les points pour lesquels les mouvements composants sont en opposition de phase ont une amplitude nulle. Ils sont au repos.
- Nombre de franges :
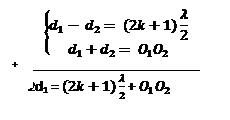 d1 =
d1 =  +
+


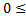 d1
d1  ⟹
⟹ 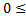
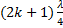 +
+ 
 ⟹
⟹ 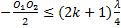
 -
- 

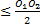 ⟹
⟹ 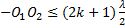
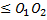 ⟹
⟹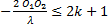
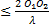
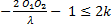
 - 1
- 1 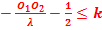
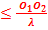
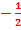
Ø Conclusion :
L’ensemble des points d’amplitude maximale est une famille d’hyperbole définie par
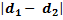 =
=  ,
, 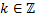
L’ensemble des points d’amplitude nulle est une famille d’hyperbole définie par
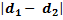 =
= 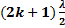 ,
, 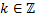
Les franges d’amplitude maximale et les franges d’amplitude nulle s’intercalent.
Dans le cas où l’amplitude n’est ni maximale, ni nulle, on a :
 ) et φ =
) et φ = 
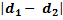 est
appelé différence de marche.
est
appelé différence de marche. 
