Topic outline
- General
- DYNAMIQUE DE TRANSLATION
DYNAMIQUE DE TRANSLATION
A- Le théorème du centre d’Inertie
1) Le vecteur quantité de mouvement
Le vecteur quantité de mouvement noté
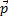 , d’un solide (système d’un point matériel) de masse m
animé d’un vecteur vitesse
, d’un solide (système d’un point matériel) de masse m
animé d’un vecteur vitesse 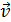 est
définie par.
est
définie par.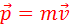
Son module vaut : ‖
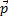 ‖= mv
‖= mvp en kg.m/s ; m en kg et v en m/s
2) Le principe d’inertie
Un système de point matériel est dit mécaniquement :
- Isole : lorsqu’il ne subit aucune force extérieure
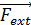 = 0
= 0- Pseudo-isole : lorsque la résultante des forces extérieure appliquées au solide est égale au vecteur nul
Ʃ
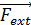 = 0
= 0
3) La relation Fondamentale de la dynamique (RFD)
Dans le repère Galiléen R(G,
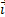 ,
, 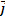 ), la résultante des forces extérieures appliquées à
un solide est égale au dérivé par rapport au temps du vecteur quantité de :
), la résultante des forces extérieures appliquées à
un solide est égale au dérivé par rapport au temps du vecteur quantité de :Ʃ
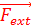 =
= 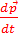
Conséquence
a) Si le système est pseudo-isolé
Ʃ
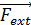 = 0⇒
= 0⇒ 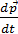 = 0⇒
= 0⇒ 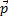 =constante.
L’égalité
=constante.
L’égalité 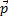 =constante indique
le théorème de la conservation du vecteur quantité de mouvement.
=constante indique
le théorème de la conservation du vecteur quantité de mouvement.Ce théorème est utilisé lors d’un choc de deux solides. Il existe deux types de chocs
- Choc Mou : après le choc les deux solides s’accrochent c.-à-d. ils sont animés à la même vitesse après le choc. Il y a conservation du vecteur quantité de mouvement (et perte d’énergie cinétique)
Ec(avant le choc) ˃ Ec (après le choc)
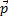 (avant le choc) =
(avant le choc) = 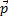 (après le choc)
(après le choc)m1
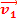 + m2
+ m2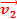 = (m1 + m2)
= (m1 + m2)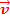
- Choc élastique : après le choc les deux solides s’écartent.C.-à-d. ils sont animés des vitesses différentes après le choc. Il y a conservation du vecteur quantité du mouvement et conservation de l’énergie cinétique.
Ec(Avant le choc) = Ec(après le choc)
m1
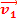 + m2
+ m2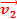 = m1
= m1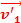 + m2
+ m2 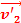
 m1
m1 +
+  m2
m2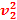 =
= m1
m1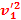 +
+ m2
m2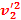
b) Si le vecteur vitesse est un vecteur variable
Ʃ
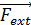 =
=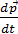 =
= 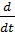 (m.
(m.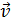 ) = m
) = m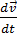
Donc, Ʃ
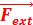 = m
= m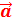
C’est la formule du théorème de centre d’inertie (ou TCI)
Remarque :
Plan à suivre lors de l’application du TCI
- Préciser le système a étudié
- Représenter les forces appliques au solide (bilan des forces appliquer ou inventorier des forces appliquer)
- Choisir un repère de projection :
· Repère Galiléen si le support de la trajectoire est rectiligne dont G
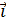 est même sens
est même sensque le mouvement et G
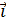 perpendiculaire à G
perpendiculaire à G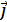
· Repère de Frènet si le support de la trajectoire est curviligne (courbe) dont G
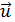 tangente à la trajectoire et même sens que le mouvement
et G
tangente à la trajectoire et même sens que le mouvement
et G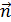 normal perpendiculaire à la trajectoire et centripète.
normal perpendiculaire à la trajectoire et centripète.- Ecrire la formule du TCI
- Projeter la formule du TCI sur le repère choisi pour résoudre le problème
B- Application
Un corps A de masse mA=70 g entraine dans sa chute un corps B de masse mB = 80g qui glisse sur un plan incliné d’un angle =30°. A et B sont reliés par l’intermédiaire d’un fil inextensible qui passe par la gorge d’une poulie dont on néglige la masse.
Calculer en négligeant tous les frottements, l’accélération et la tension du fil (g=10 ms-2)

Système : corps B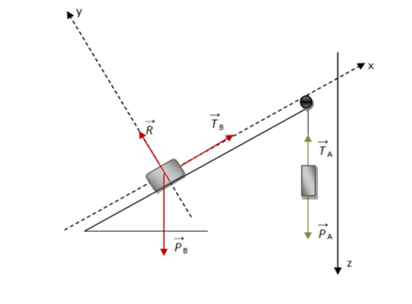
Référentiel : terrestre
Bilan des forces :
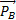 ,
, 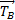 ,
,TCI :
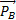 +
+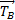 +
+= mB
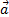
Projetons la relation vectorielle sur l’axe Ox:
-PBsinα + TB = mBa ⇒ TB = mB(a + g sinα) (1)
Système : corps A
Référentiel : terrestre
Bilan des forces :
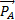 ,
, 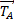
TCI :
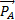 +
+ 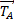 = mA
= mA 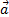
(0z) : - PA + TA = mAa⇒ TA = mA(g – a) (2)
La tension du fil inextensible est partout la même: TA= TB
mA(g – a) = mB (a + g sinα)
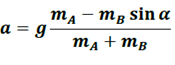
AN: a=2 m.s-2
La tension des fils: TB= TA= mA (g-a) =0,56 N
C- Applications aux mouvements plans
1. Mouvement d’un projectile dans le champ de pesanteur
Un projectile S de masse m est lancée dans le champ de pesanteur à partir d’un point O considéré comme origine des espaces avec une vitesse V0 faisant un angle α avec l’horizontale.

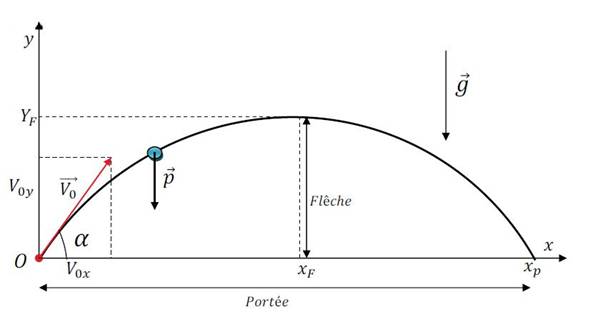
On appelle portée, l’abscisse xp d’un projectile, le point P d’ordonné nulle (c’est le point de chute du projectile).
On appelle flèche, la hauteur maximale h atteinte par le projectile.
1- Déterminer les équations horaires et de la trajectoire de ce projectile.
2- Calculer la portée et la flèche.
Résolution :
Système : SolideRéférentiel : Terrestre
Représentation du système
1- Les équations horaires et l'équation cartésienne de la trajectoire:
Ʃ
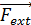 = m
= m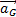
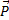 = m
= m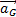
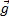 =
=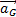
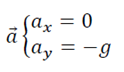
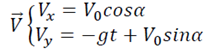
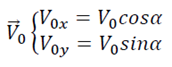
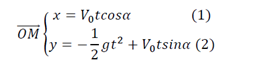
Pour déterminer l’équation de la trajectoire on remplace le temps dans l’équation horaire y(t).

2. Calcul de la flèche et de la portée:
La portée correspond à l’ordonnée nul donc y=0
Soit la portée de point P (O, xP) en posant y=0 dans l’équation de la trajectoire on obtient :
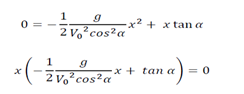
Donc après calcul on obtient x = 0 ou
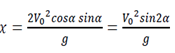
On retiendra donc que la portée à pour valeur
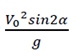
Calcul de la flèche
La trajectoire étant parabolique, l’abscisse de la flèche est égale à la moitié de celle de la portée, donc :
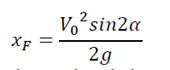
Nous remplaçons cette expression dans l’équation de la trajectoire c.à.d.
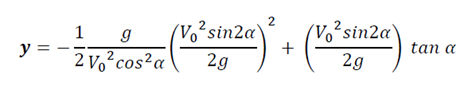
Par transformation, on obtient :
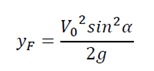
2- Mouvement d‘une particule chargée dans un champ électrostatique uniforme
On considère un champ électrostatique uniforme
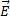 produit par deux plaques parallèles
produit par deux plaques parallèles(A) et (B) entre lesquelles il est établi une différence de potentiel VA = VB constante. Une particule de charge q lancées d’un point O dans le champ avec une vitesse V0 est soumise à la force électrostatique
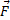 . Le poids de la charge est négligeable devant
. Le poids de la charge est négligeable devant 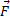 .
.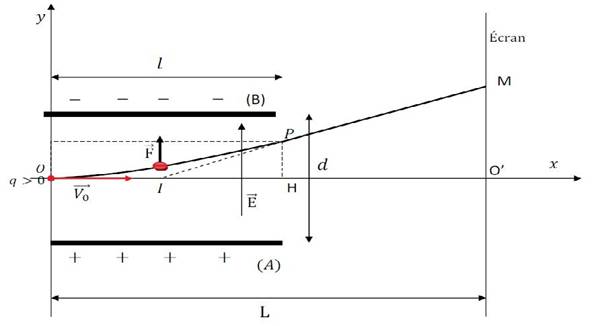

La vitesse initiale V0 est horizontale et à l’instant t=0 la particule de charge positive entre en O(0,0). Ecrire les équations paramétriques du mouvement et déduire l’équation de la trajectoire. Puis calculer la déflexion ou déviation linéaire c'est-à-dire l’ordonnée de la tache sur l’écran.
Système : particule chargée
Référentiel : Terrestre
Représentation du système
Le TCI nous donne
Ʃ
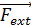 = m
= m 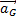
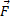 = m
= m 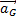 n’ayant pour seule force que la force électrique
n’ayant pour seule force que la force électriqueNous obtenons comme accélération
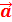 =
= 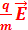
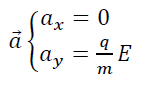
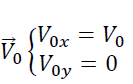
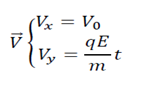
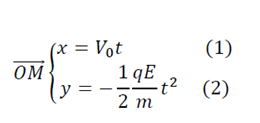
Equation de la trajectoire :
x = v0t ⇒ t =

Donc,
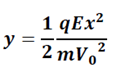
A la sortie des armatures, on est au point P c'est-à-dire x=l et y=HP. Pour trouver l’ordonnée M de l’impact sur l’écran, on utilise les triangles IMO’ et IPH.
On pose
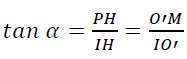
Ce qui nous permet d’écrire
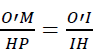
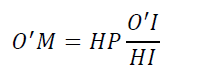
Ceci nous permet au final d’avoir
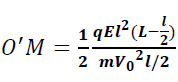
Au final on obtient
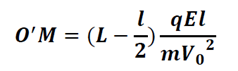
D- Oscillateurs en translation
1. PENDULE ELASTIQUE HORIZONTAL
On suppose que la masse m glissant sans frottement sur un plan horizontal est reliée à l’une des extrémités d’un ressort de raideur k, l’autre extrémité étant fixe. Soit le repère (G, 0,
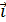 )
)
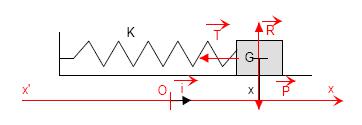
a) Équation différentielle du mouvement
Système : la masse m
Référentiel : laboratoire
Bilan des forces : R,P etT
Théorème du centre d’inertie :
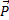 +
++
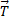 =m
=m 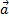
Projetons la relation vectorielle sur l’axe xx’ :
0 + 0 – T = m
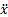 avec T = kx
avec T = kx- kx = m
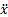
Donc,
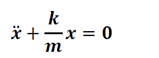
C’est l’équation différentielle d’un mouvement harmonique.
c) Solution de l’équation différentielle

d) étude énergétique
Un instant t donné:
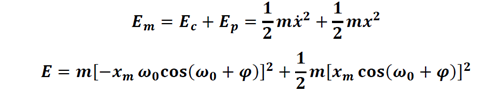
Le système est conservatif car l’énergie mécanique est constante.
2. PENDULE ELASTIQUE VERTICAL
a) équation différentielle
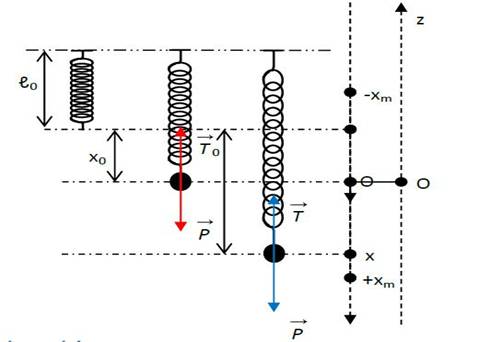

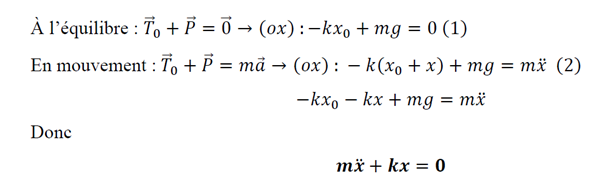
b) étude énergétique
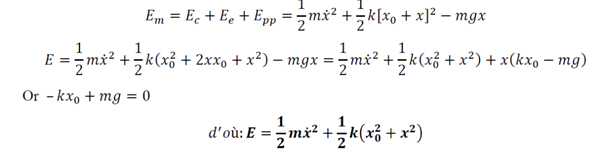
L’énergie mécanique se conserve: le système est conservatif car l’énergie est constante
3. PENDULE ELASTIQUE SUR UN PLAN INCLINE
a) étude dynamique

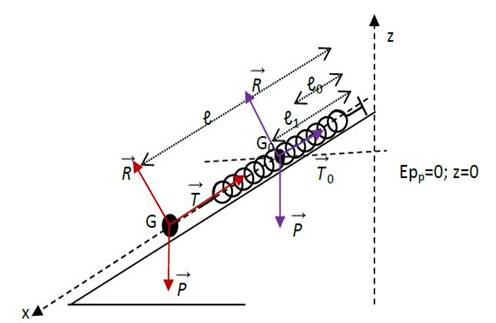
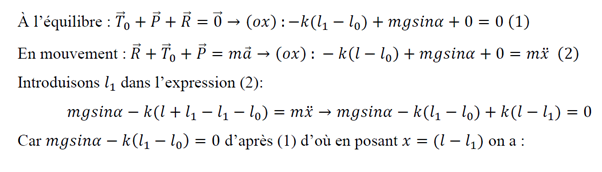
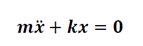
b) étude énergétique
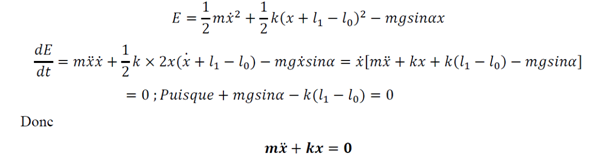

Mr RANDRIANANTENAINA Chabanas Deloy
e mail: deloychabanas@gmail.com
