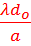Themen dieses Kurses
- Allgemeines
- Chap I NATURE ONDULATOIRE DE LA LUMIERE
Chap I NATURE ONDULATOIRE DE LA LUMIERE
Chap I : NATURE ONDULATOIRE DE LA LUMIERE : INTERFERENCES LUMINEUSES
1- Propriétés de la lumière :
- La lumière est une onde électromagnétique transversale.
- Une lumière polychromatique est constituée par plusieurs radiations, elle se décompose par un prisme.
Exemple : lumière blanche

Source : http://lewebpedagogique.com/blog21quatrieme/2015/02/12/la-decomposition-de-la-lumiere-blanche/ :
- Une lumière monochromatique est constituée par une seule radiation (une seule longueur d’onde), elle ne se décompose pas par un prisme, elle a une couleur autre que la couleur blanche (rouge, jaune, orange, bleue, verte, …)
2- Interférences lumineuses :
Le phénomène d’interférences lumineuses est obtenu par superposition des radiations provenant de deux sources lumineuses cohérentes et synchrones S1 et S2 réelles ou virtuelles par la lumière provenant d’une source unique S.
Pour les dispositifs expérimentaux, on peut citer : fentes d’Young, miroir de Fresnel, biprisme de Fresnel, bilentille de Billet, …
a) Fentes d’Young :
Expérience :
Une source de lumière monochromatique S a éclairé les deux fentes d’young identiques F1 et F2. Les deux faisceaux provenant de F1 et F2 présentent une partie commune appelée : champ d’interférence (ou zone d’interférence)
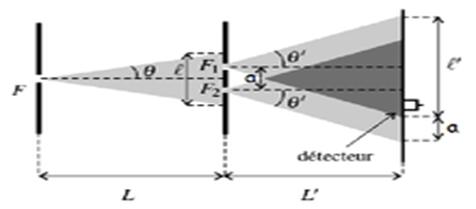
Phénomène observé :
On observe sur l’écran, entre I1 et I2 des franges de lumière ayant la forme d’arc hyperbole alternativement brillante et obscure appelées : franges d’interférences
Interprétation :
A chaque lumière monohcromatique, on associe une onde sinusoïdale de longueur d’onde λ=vT
y(t)= a sin (ωt + φ)
Par conséquent, les fentes F1 et F2 constituent deux sources de lumière monochromatiques de même amplitude, de même fréquence et en phase.
Posons φ= 0, yF1(t) = yF2(t) = a sin (
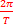 t)
t)En un point M d’interférence, on peut établir que :
YM(t) = 2a cos
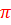 (
(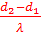 )sin[
)sin[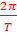 t –π (
t –π (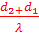 )]
)]Schéma équivalent de la fente d’Young :
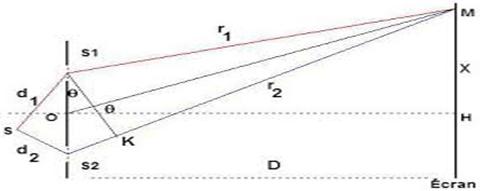
La différence de marche pour atteindre le point M est 𝚫 = d2-d1
𝚫 = d2-d1 =
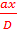
§ Si 𝚫 = d2-d1 = kλ, les deux vibrations composantes sont en phase au point M et l’amplitude de la vibration résultante Y est maximale. Les franges correspondantes sont brillantes.
Abscisses des franges brillantes :
d2-d1= kλ, kϵ
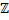
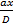 =
kλ
=
kλx = k
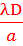 , kϵ
, kϵ 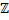
Pour k = 0, x = 0 ⇒ la frange centrale est brillante
§ Si 𝚫 = d2-d1 = (2k + 1)
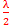 ,
les deux vibrations composantes sont en opposition de phase au
point M et l’amplitude de la vibration résultante Y est nulle. Les franges
correspondantes sont sombres.
,
les deux vibrations composantes sont en opposition de phase au
point M et l’amplitude de la vibration résultante Y est nulle. Les franges
correspondantes sont sombres.Abscisses des franges sombres :
d2-d1 = (2k + 1)
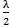

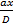 =
(2k + 1)
=
(2k + 1)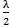
x = (2k + 1)
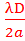 , kϵ
, kϵ 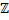
Interfrange :
On appelle interfrange, la distance qui sépare le milieu de deux franges consécutives de même nature. Elle est notée par i.
Soit deux franges brillantes consécutives de numéro k et k+1
i = xk+1 - xk
i = (k+1)
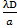 -
k
-
k 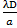
i = k
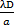
i =
 ⇒ λ =
⇒ λ = 
b) Miroirs de Fresnel :
Ils sont constitués par deux miroirs plans rectangulaires m1 et m2 qui sont juxtaposés de façon qu’un de leurs bords O soit commun et tel que m1 et m2 font un angle α petit (de l’ordre de quelques minutes)
Expérience :
Une source de lumière monochromatique S, supposée ponctuelle, éclaire la totalité de leurs faces réfléchissantes sous une incidence rasante.
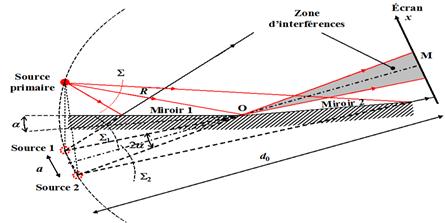
Source : http://www.optique-ingenieur.org/fr/cours/OPI_fr_M02_C05/res/Fig_02.jpg
Aux deux faisceaux incidents juxtaposés, les miroirs font correspondre deux faisceaux réfléchis qui présentent une partie commune appelée : champ d’interférence.
Les deux faisceaux réfléchis semblent provenir des sources S1 et S2, images virtuelles de la source S, symétrique de celle-ci par rapport aux plans des deux miroirs.
S, S1 et S2 se trouvent sur un même cercle de centre O.
Phénomène observé :
On observe sur l’écran (E), dans la partie commune aux deux faisceaux, des raies équidistantes alternativement brillantes et sombres appelées : franges d’interférence.
Interprétation :
Les deux sources virtuelles S1 et S2 constituent deux sources de vibration sinusoïdales vibrant avec la même période et en phase.
yS1(t) = yS2(t) = a sin (
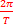 t)
t)On dit que S1 et S2 sont deux sources cohérentes.
Soit M un point quelconque du champ d’interférence. L’état vibratoire du point M ne dépend que des distances S1M=d1 et S2M=d2 du point M aux deux sources S1 et S2.
Δ=d2-d1= est la différence de marche.
§ Si Δ=d2-d1=kλ, les deux vibrations composantes sont en phase au point M et l’amplitude de la vibration résultante Y est maximale. Les franges correspondantes sont brillantes.
Abscisses des franges brillantes :
d2-d1= kλ, kϵ
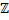
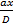 =
kλ
=
kλx = k
 , kϵ
, kϵ 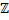
Pour k = 0, x = 0 ⇒ la frange centrale est brillante
§ Si 𝚫 = d2-d1 = (2k + 1)
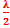 ,
les deux vibrations composantes sont en opposition de phase au
point M et l’amplitude de la vibration résultante Y est nulle. Les franges
correspondantes sont sombres.
,
les deux vibrations composantes sont en opposition de phase au
point M et l’amplitude de la vibration résultante Y est nulle. Les franges
correspondantes sont sombres.Abscisses des franges sombres :
d2-d1 = (2k + 1)
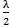
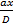 =
(2k + 1)
=
(2k + 1)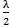
x = (2k + 1)
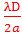 , kϵ
, kϵ 
Les milieux des franges de même nature sont équidistants de i =

Largeur du champ d’interférence :
tan α =
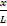 ≈ α
(α petit, tan α ≈ α)
≈ α
(α petit, tan α ≈ α)x = L α ⇒
 = L α ⇒
l = 2L α
= L α ⇒
l = 2L αl est la largeur du champ d’interférence.
c) Biprisme de Fersnel :
Il est constitué par deux prismes de verre identiques d’angle  d’indice n collés par leur base ayant une face commune.
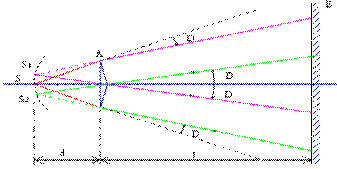
Source : http://uel.unisciel.fr/physique/interf/interf_ch02/co/apprendre_ch2_02.html
La fente source S est placée perpendiculairement au plan de section principale du dispositif, sur l'axe du système. Elle éclaire chaque prisme de manière identique qui en donne une image virtuelle supposée stigmatique. On obtient ainsi deux sources virtuelles secondaires S1 et S2.
Tous les rayons arrivant sur un prisme sont déviés d'une même quantité
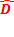 = (n-1)
= (n-1) 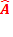 vers la base du
prisme. Tout se passe comme si l'on avait deux fentes sources S1 et
S2 obtenues par une rotation d'angle
vers la base du
prisme. Tout se passe comme si l'on avait deux fentes sources S1 et
S2 obtenues par une rotation d'angle 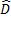 vers les sommets
des prismes.Les interférences s'observent dans la partie commune aux deux
faisceaux semblant provenir de S1 et S2.
vers les sommets
des prismes.Les interférences s'observent dans la partie commune aux deux
faisceaux semblant provenir de S1 et S2. 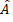 :
angle du prisme (en rad)
:
angle du prisme (en rad)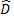 :
angle de déviation du rayon réfracté
:
angle de déviation du rayon réfracté
n : indice de réfraction du prisme
tan
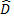 =
= 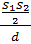 =
= 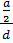 ≈
≈ 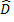 (
(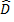 petit,
tan
petit,
tan 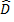 ≈
≈ 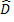 )
)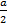 =
= 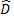 ⇒a = 2
⇒a = 2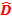 d
d- Largeur du champ d’interférence :
tan
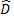 =
= 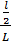 =
= 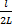
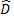 petit,
tan
petit,
tan 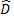 ≈
≈ 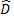 =
= 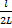 ⇒l = 2L
⇒l = 2L 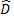
l : largeur du champ d’interférence
- Interfrange :
i =
 =
= 
d) Bilentille de Billet :
Une lentille mince convergente est divisée en deux suivant le petit diamètre. Les deux moitiés sont légèrement écartées l’une de l’autre.
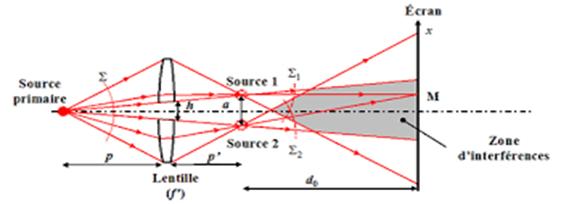
Source : http://www.optique-ingenieur.org/fr/cours/OPI_fr_M02_C05/co/Contenu_14.html
Chaque demi-lentille donne sa propre image de la source primaire. Chaque image constitue donc une source secondaire. L’écran est placé à la distance d0 des sources secondaires, soit à la distance d0+p’ de la bilentille. Si la bilentille est écartée de la quantité h et la source primaire placée à la distance p, alors les sources secondaires sont situées à la distance p’, et elles sont écartées de la quantité a.
S1 et S2 sont les images réelles de S par les deux demi-lentilles.
Comme précédemment, nous observons les interférences entre deux fronts d'ondes sphériques émis par deux sources de même amplitude et en tout point M dans la zone d’interférence.
L’interfrange est
i =
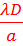 =
=